Quick Links

Overview

This is the first study on crowdsourcing Pareto-optimal object finding, which has applications in public opinion collection, group decision making, and information exploration. Departing from prior studies on crowdsourcing skyline and ranking queries, it considers the case where objects do not have explicit attributes and preference relations on objects are strict partial orders. The partial orders are derived by aggregating crowdsourcers’ responses to pairwise comparison questions. The goal is to find all Pareto-optimal objects by the fewest possible questions. It employs an iterative question selection framework. Guided by the principle of eagerly identifying non-Pareto optimal objects, the framework only chooses candidate questions which must satisfy three conditions. This design is both sufficient and efficient, as it is proven to find a short terminal question sequence. The framework is further steered by two ideas— macro-ordering and micro-ordering. By different micro-ordering heuristics, the framework is instantiated into several algorithms with varying power in pruning questions. Experiment results using both real crowdsourcing marketplace and simulations exhibited not only orders of magnitude reductions in questions when compared with a brute-force approach, but also close-to-optimal performance from the most efficient instantiation.



Consider a set of objects O and a set of criteria C for comparing the objects. An object x∈O is Pareto-optimal if and only if x is not dominated by any other object, i.e., ∄y∈O such that y≻x. An object y dominates x (denoted y≻x) if and only if x is not better than y by any criterion and y is better than x by at least one criterion, i.e., ∀c∈C : x ⊁c y and ∃c∈C : y ≻c x. If x and y do not dominate each other (i.e., x⊁y and y⊁x), we denote it by x∼y. The preference (better-than) relation Pc (also denoted ≻c) for each c∈C is a binary relation subsumed by O×O, in which a tuple (x, y)∈Pc (also denoted x ≻c y) is interpreted as “x is better than (preferred over) y with regard to criterion c”. Hence, if (x, y)/∈Pc (also denoted x ⊁c y), x is not better than y by criterion c. We say x and y are indifferent regarding c (denoted x ∼c y), if (x, y)/∈Pc ∧ (y, x)/∈Pc. We consider the setting where each Pc is a strict partial order as opposed to a bucket order [1] or a total order, i.e., Pc is irreflexive (∀x : (x, x) /∈ Pc) and transitive (∀x, y : (x, y)∈Pc ∧ (y, z)∈Pc ⇒ (x, z)∈Pc), which together imply asymmetry (∀x, y : (x, y)∈Pc ⇒ (y, x)/∈Pc). We note that such definition of better-than relation has been widely used in modeling preferences (e.g., [10, 2, 5]). Pareto-optimal object finding lends itself to applications in several areas, including public opinion collection, group decision making, and information exploration, exemplified by the following motivating examples.

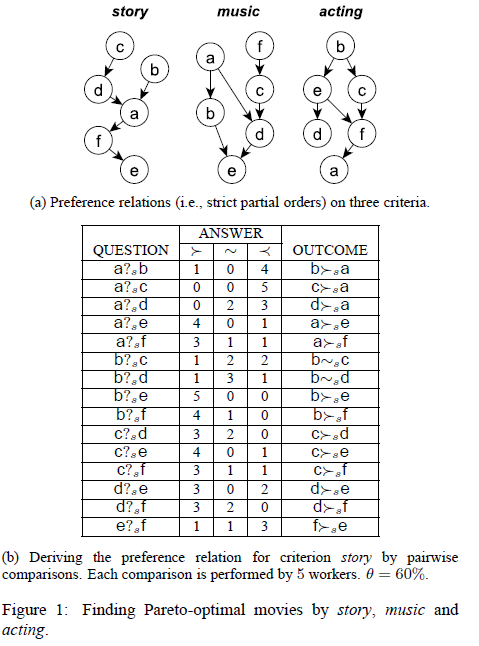
• Example 1 (Collecting Public Opinion and Group Decision Making). Consider a set of movies O={a,b,c,d,e,f} and a set of criteria C={story, music, acting} (denoted by s, m, a in the ensuing discussion). Fig.1a shows the individual preference relations (i.e., strict partial orders), one per criterion. Each strict partial order is graphically represented as a directed acyclic graph (DAG), more specifically a Hasse diagram. The existence of a simple path from x to y in the DAG means x is better than (preferred to) y by the corresponding criterion. For example, (a, e)∈Pm (a ≻m e), i.e., a is better than e by music. (b, d)/∈Ps and (d, b)/∈Ps; hence b ∼s d. The partial orders define the dominance relation between objects. For instance, movie c dominates d (c≻d), because c is preferred than d on story and music and they are indifferent on acting, i.e., c ≻s d, c ≻m d, and c ∼a d; a and b do not dominate each other (a∼b), since b ≻s a, a ≻m b and b ≻a a. Based on the three partial orders, movie b is the only Pareto-optimal object, since no other objects dominate it and every other object is dominated by some object.

  Note that tasks such as the above one may be used in both understanding the public’s preference (i.e., the preference relations are collected from a large, anonymous crowd) and making decisions for a target group (i.e., the preference relations are from a small group of people).

• Example 2 (Information Exploration). Consider a photography enthusiast, Amy, who is drown in a large number of photos she has taken and wants to select a subset of the better ones. She resorts to crowdsourcing for the task, as it has been exploited by many for similar tasks such as photo tagging, location/face identification, sorting photos by (guessed) date, and so on. Particularly, she would like to choose Pareto-optimal photos with regard to color, sharpness and landscape.

  By definition, the crux of finding Pareto-optimal objects lies in obtaining the preference relations, i.e., the strict partial orders on individual criteria. Through crowdsourcing, the preference relations are derived by aggregating the crowd’s responses to pairwise comparison tasks. Each such comparison between objects x and y by criterion c is a question, denoted x ?c y, which has three possible outcomes—x ≻c y, y ≻c x, and x ∼c y, based on the crowd’s answers. An example is as follows.

• Example 3 (Deriving Preference Relations from Pairwise Comparisons by the Crowd). Fig.1b shows the hypothetical results of all 15 pairwise comparisons between the 6 movies in Example 1, by criterion s=story. The outcomes of all comparisons form the crowd’s preference relation on story (the leftmost DAG in Fig.1a). Fig.2 is the screenshot of a question form designed for one such comparison. A crowdsourcer, when facing this question, would make a choice among the three possible answers or skip a question if they do not have enough confidence or knowledge to answer it. Fig.1b shows how many crowdsourcers have selected each answer. For instance, for question a ?s f, three people preferred movie a, one person preferred f, and one person is indifferent. By aggregating these answers, it is derived that a is better than f with regard to story, since 60% of the crowdsourcers who responded to the question chose this answer. For question b ?s c, the result is b ∼s c, since neither b ≻s c nor b ≺s c received enough votes. (Assuming a threshold θ=60%, i.e., either b ≻s c or b ≺s c should have at least 60% of votes, in order to not declare b ∼s c.)