Quick Links

Overview

CrewScout is a system for finding expert teams in accomplishing tasks. The underpinning concept of the system is skyline teams or skyline groups, which we introduced in a CIKM12 paper and a TKDE paper.

Consider a set D of n experts t1, ..., tn, modeled by m numeric attributes A1, ..., Am that represent their skills and expertise. Any subset of k experts form a k-expert team. CrewScout finds, for a given k, all k-expert skyline teams, i.e., k-expert teams that are not dominated by any other k-expert teams. It further assists users in choosing among the skyline teams. The notion of dominance between teams is analogous to the dominance relation between tuples in skyline analysis. CrewScout calculates for each team an aggregate vector of its experts’ individual vectors. CrewScout provides efficient algorithms for four commonly used aggregate functions—AVG (i.e, SUM, since we only compare teams with equal size), MIN and MAX. A team G1 dominates another team G2 (denoted G1 ≻ G2), if and only if the aggregate value of G1 on every attribute is better than or equal to the corresponding value of G2 and G1 has better value on at least one attribute.

The need for finding expert teams prevails in several application areas, including question answering, crowdsourcing, panel selection, project team formation, and so on. This is illustrated by the following motivating examples.


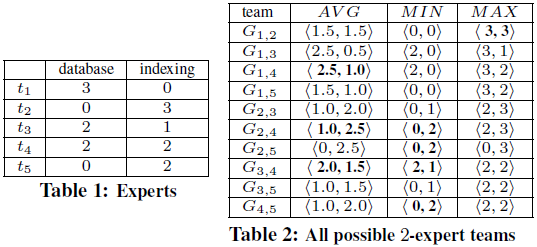
• CrowdSourcing Consider forming a team of Wikipedia editors to write a newWikipedia article related to “database” and “indexing”. Table 1 shows all relevant editors t1, . . . , t5 and their expertise on the two topics. We want to assign the task to a team of 2 editors. Table 2 shows the aggregate vectors under AVG, MIN and MAX, for all possible 2-expert teams where Gi,j stands for a team of experts ti and tj. A simple scheme such as picking top editors on individual topics does not work. For example, G1,2 consists of the top editor on each topic and has an aggregated vector <1.5, 1.5> with regard to AVG. G3,4, with vector <2.0, 1.5>, dominates G1,2 (denoted G3,4≻G1,2) under AVG. Hence, G3,4 is a better team in terms of collective expertise. In fact, G3,4 is a 2-expert skyline team, since no other team dominates it under AVG. Table 2 highlights all 2-expert skyline teams for every aggregate function.
• Questing Answering: Consider a question-answering platform such as Quora.com. A question is displayed to users who might answer it. The question asker can also explicitly solicit answers from certain users, oftentimes by offering rewards. To receive quality answers, it is necessary to intelligently post the question to users with proper expertise. More often than not, a question requires expertise on several aspects that cannot be fulfilled by any single user, needing attention from a diverse team of experts who collectively excel. For instance, consider question “Is C or Python better for high-performance computing?” To get a comprehensive answer, we need experts in “high performance computing”, “C”, and so on.
• Other Motivating Applications The need for finding expert teams arises in several other applications. 1) Consider the task of choosing a panel of experts to evaluate a research paper or a grant proposal. An expert can be modeled as a tuple in the multi-dimensional space defined by the paper’s topics, to reflect the expert’s strength on these topics. The collective expertise of a panel is modeled as the aggregate vector of the corresponding tuples. 2) Forming collaborative teams for a software development project can be viewed as finding programmers who are collectively strong in the multidimensional space of desired skills for the project. 3) In a variety of applications we look for “teams” in more general sense, such as bundles of products, reviews, stocks, and so on. For instance, to summarize a product’s many customer reviews, choosing a set of diverse reviews is forming a “team” of reviews, where the reviews are modeled by attributes such as “sentiment”, “length”, “quality”, etc. Another example is online fantasy sports where gamers compete by forming and managing team rosters of real-world athletes, aiming at outperforming other gamers’ teams. The teams are compared by aggregated statistics (e.g., “points”, “rebounds”, “assists” in basketball games) of the athletes in real games.

An attractive characteristic of a skyline team is that no other team of equal size can dominate it. In contrast, given a non-skyline team, there is always a better skyline team. This property distinguishes CrewScout from other team recommendation techniques. The skyline teams consist of the teams that are worth recommending. They become the input to further manual or automated post-processing that eventually finds one team. Admittedly, determining the “best” team is a complex task that may involve more factors than what skyline teams can capture—e.g., which experts are available for a task, whether they have good relationship to work together, and so on. The post-processing is thus crucial. Examples of such post-processing include eye-balling the skyline teams, filtering and ranking them by user preferences, and browsing and visualization of the skyline teams. Particularly, CrewScout provides an interactive tool to assist a human user in exploring and choosing skyline teams.